最近積の和典型が話題になっているので書きます。
N個のマス目が横一列に並んでいる状況を考えます。初め、全部のマスは白色です。このうち K 個のマスを選んで黒く塗った時にできるマスの状態は何通りでしょうか?

これは 通りです。
これを応用すると、次のような問題が解けます。
長さが N であって、総和が M である非負整数列の個数を求めよ。
非負整数列というのは、各要素が負の数でない整数からなる数列です。[1, 2, 3, 4, 5] とか [0, 0, 1, 4, 3] とかです。これの個数を数えるのに、先ほどのマスの数え方を使うことができます。
まず、 M + N - 1 個の白いマス目を用意します。そのあと、そこから N - 1 マス選んで塗ります。こうしたとき、必ず M 個のマスが白いままで残っています。また、マスの両端や黒マスを境目として考えると、白いマスが連続するような区間は N 個の部分に分かれます。(黒いマスが連続するような塗り方もありますが、その時は白いマスが0個の部分があると解釈します)
ここで、それぞれの部分について白いマスの連続する個数を数えると、長さ N の数列ができます。白いマスは全部で M 個なので、これは総和が M で長さ N の数列となり、求めたいものの1つとなっています。
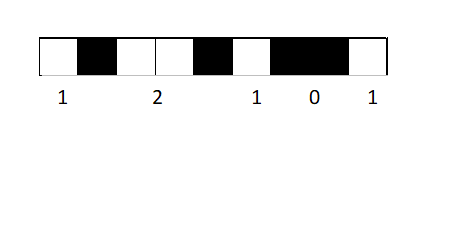
また、塗り方と数列は一対一対応します。つまり、ある塗り方からできる数列はちょうど1つであって、ある数列から復元できる塗り方もちょうど1つであるということです。よって、数列の個数を数える代わりに塗り方を数えてもいいことになります。
塗り方は、 M + N - 1個のマス目から N - 1 個を選んで塗る方法なので、通りです。
発展テク: 「総和が M 以下」の場合、数列の後ろに追加で 1 つダミーの値があるとします。数列の総和が M より小さかった時は、このダミーに押し付けると考えると、解くことができます。
長さが N であって、総和が M である非負整数列
すべてに対して
を計算した時の総和を求めよ。
今回の本題です。
は総積記号で、数列 A の要素を全部掛け算してねという意味です。その掛け算を A としてあり得るもの全部でやって、それを足してねという問題です。
さて、これを解くためにいくつか準備をします。まず、A_i を掛けるという操作は、A_i 個のマスから 1 つ選んで塗る方法と対応付けることができます。
例えば下の図のように、複数のマスが並列して並んでいる場合を考えるとわかりやすいと思います。

この考え方と、先ほどの非負整数列の数え方を組み合わせます。
まず、 M + N - 1 個の白いマス目を用意して、そのうち N - 1 個を黒く塗ります。ここまではさっきと同じです。先にも言ったとおり、どんな塗り方をしたとしても、白いマス目からなる N 個の区間ができます。その N 個の区間から 1つずつマスを選んで、赤く塗ることにします。

長さ 0 の区間ができたときは赤に塗るマスが無いので困りますが、そのようなときはどうせ掛け算すると0になるので無視できます。これを無視した時、マス目には赤色と黒色を合わせて N - 1 + N = 2N - 1 マスの色のついたマスが存在することになります。(初めに塗った黒マス N - 1 個 + N 個の区間それぞれで塗った赤マス N 個)
このように塗ってできるマスの状態の総数は、求めたい答えと一致します。
ここで、重要な考察をします。初めにどんな黒の塗り方をしても、後でどんな赤の選び方をしても、マスを左から見たときに、色のついたマス目の色は赤、黒、赤、…、黒、赤の順番で並びます。なので、もしマス目の色が赤と黒どちらか分からなくなってしまったとしても、色のついたマスがどこにあるかさえ分かれば、色を一通りに復元することができます。よって、実は赤と黒を区別する必要はなく、一緒くたにしてしまってよいことになります。よって、このような塗り方は M + N - 1 個のマスから 2N - 1 個選ぶ方法、 通りです。
発展テク: 「総和が M 以下」の場合、さっきと同様に、数列の後ろに追加で 1 つダミーの値があるとします。また同様に数列の総和が M より小さかった時は、このダミーに押し付けると考えますが、ダミーの値の部分を掛けることはないので、ここを赤く塗ることはありません。よって、塗るべきマスの個数は 2N 個になります。